Fluid mechanics

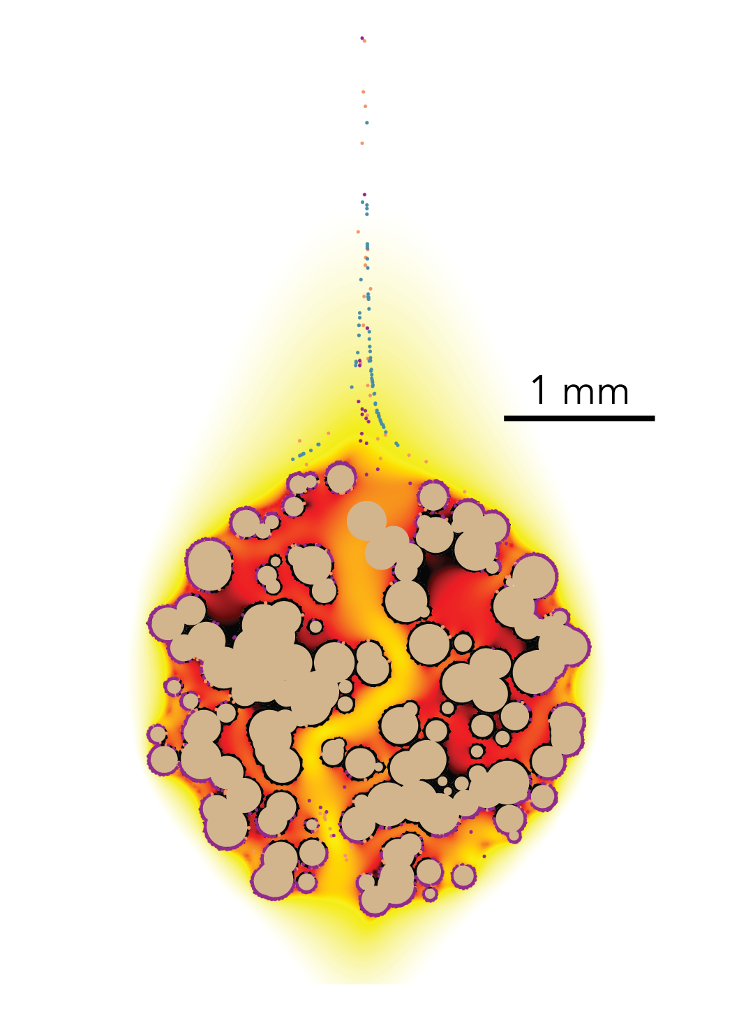
There are two length scales we care about: Planetary and Micro. More or less both ends of the spectrum (yes, admittedly, we’re not spanning subatomic particles to the universe, but cut us some slack, please). At the microscale, we’ve conducted a number of experiments in the lab to understand how marine snow particles develop, and in order to extend our empirical data to the real world, we use a variety of tools to model our systems.

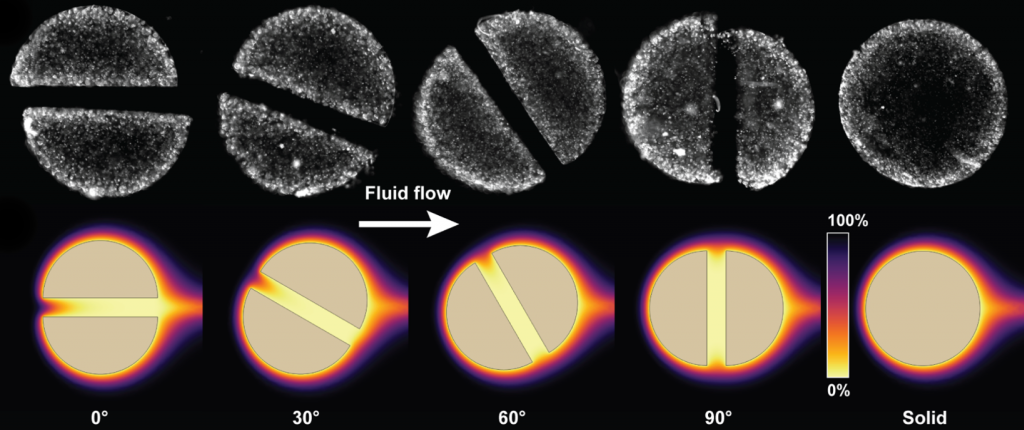
Taken from Shen et al. (2023), the top row shows real bacterial growth in a particle with a macropore subjected to bulk fluid flow. The bottom row shows the same system but modeled dissolved oxygen concentrations. The angle of the channel relative to the bulk flow dictates the importance of advection vs. diffusion in resupplying this limiting resource, allowing differences in microbial growth to manifest.

Multiphysics finite difference models are quite nice for solving the fluid flow equations and mapping chemical and biological transformations onto the physical diffusion and advection fields. There are two major packages we’ve used, FEATool (a Matlab package) and COMSOL. Bottom line: we’ll use whatever we need to serve the purpose of our scientific goals!

Velocity field through a hypothetical porous marine particle sinking in the ocean. Yellow is high, red/back are slow. The bacteria (dots) interact with this flow to either attach to the particle or be swept through and around it into the plume. From Borer et al. (2022)